Shell Theory:
Statistics in High Dimensions

Introduction

The problem of interpreting high dimensional data has long bedeviled our machine learning community and resulted in a confusing array of proofs and counter-proofs. Our paper attempts to create an overarching framework for thinking about high dimensional data, in the hope of bringing some consistency to the current debate. Before introducing our ideas, we briefly summarize the current problems with high dimensions and it's impact on machine learning:

1. Interesting concepts are often high dimensional: A cat is not defined by any one attribute. Rather, the concept of cat only emerges when many attributes are considered simultaneously. This makes the cat concept innately high dimensional. As many (most?) important concepts are high dimensional, progress in machine learning is heavily reliant on a good understanding of high dimensions.
2. A curse in high dimensions? Many pattern analysis techniques are ill-conditioned in high dimensions. The problem is so prevalent that researchers have come to think of high dimensions as being cursed. There is even a famous mathematical proof of the curse [3], that is sometimes termed contrast-loss.
3. A blessing in high dimensions? Strangely, the constraints used to prove the curse become a blessing if the problem is changed slightly [2].
4. Inconsistent literature: While individual papers are internally consistent the overall literature is frustratingly inconsistent. High dimensions cannot be both curse and blessing.
5. Machine learning's crisis of interpretablity: Many machine learning problems involve high dimensions. The inconsistency of high dimensional literature makes formal analysis of machine learning algorithms difficult and may have caused machine learning's current crisis of interpretablity.

We propose a statistical framework for analyzing high dimensional data, which we term shell theory. From a theoretical perspective, shell theory resolves many of the contradictions that plague high dimensions. From a practical perspective, shell theory makes deep-learned features more interpretable; this allows a generic network to be adapted to many different machine learning problems without the requirement of explicit retraining. Paper, Github (Python Code)

An Intuitive Understanding of High Dimensions

We argue that although traditional statistical analysis is often degenerate in high dimensions, the problem is rooted in the statistical approaches used, rather than the innate inamicability of high dimensions to statistical analysis.

1. Vastness makes sparseness: Other things being equal, the volume of a sample space will increase exponentially with the number of dimensions. This makes high dimensional sample spaces vast. To understand the sheer scale of such sample spaces, we return to pondering the nature of cats. Each cat that is born / created, it is almost-surely unique. This suggests the sample space of cats is so vast that most potential cats never exist. Thus, even if a dataset contained every cat in existence, the dataset would only populate the cat sample space sparsely.
2. Sparsity is the enemy of density: From a statistical perspective, sparsity is troubling because the absence of an instance no longer implies it is unlikely to occur. This breaks the link between the density estimated from a dataset and likelihood of occurrence, that many statistical frameworks rely on. More formally, we are arguing that many of the problems associated with high dimensions arise because traditional statistical concepts like density / probability density, are ill defined in high dimensions.
3. Distance as a solution to sparsity: High dimensions makes traditional density based analysis difficult; however, it greatly simplifies distance based statistics. Huge sample spaces make coincidental similarity between two instances becomes almost-impossible. Thus distance can become a proxy for statistical dependency and vice versa. Our paper shows how this intuition can be used to formally relate instances to labels.

This perspective of high dimensions suggests that if the data generative process is modeled appropriately, the relationship between instances can be revealed through statistical analysis of their mutual distances.

Hierarchical Generative Model

If we assume data is the outcome of a series of generative processes and semantics are symbolic labels for individual generative processes, machine learning can be formulated as the problem of assigning individual instance to their generative process of origin. If the underlying generative model is appropriate, this approach allows for highly interpretable machine learning. We propose suggest that image data can be modeled as the outcome of a high dimensional hierarchical generative process.

In a hierarchical generative process, all data is considered the outcome of some generator-of-everything. However, the generator-of-everything does not generate individual instances directly. Instead, it generates child generators, which can in turn act as parents of new child generators. Any two generators are considered independent, given their parent generator. Individual instances are outcomes of the final layer of generators. The hierarchical generative model has two advantages:

1. A hierarchical generative model captures naturally occurring statistical dependencies: If we consider a pair of siblings, their appearance will likely be too similar for us to model them as independent outcomes of a human generator. However, it is reasonable to consider them independent outcomes of their parents. A hierarchical generative model captures such dependencies which are absent from traditional generative models that typically assume all generative processes are mutually independent.
2. Interpretability: A high dimensional hierarchical generative model leads to a series of theorems that make machine learning remarkably simple.

Shell Theory

In high dimensions, the distance between instances of two, independent generative processes, is almost-surely a constant, the value of which is determined by the mean and variances of the underlying generative processes [2]. Shell theory leverages this result to show that in a high dimensional, hierarchical generative:

1. Distinctive-Shell: There exist a distinctive-shell centered on the mean of each generative process that almost-surely encapsulates all instances of the process and excludes almost-all other instances. Distinctive-shells are likely the semantic manifolds that machine learning algorithms are implicitly trying to discover.
2. Shell Normalization: Having a mathematical representation of the semantic manifold means we can mathematically analyze the the impact of per-processors like normalization. The analysis suggests that the traditional normalization procedure is flawed, as it treats the training data's mean as a normalization vector. This is only effective in the special case where training and test data can be assumed to derive from the same distribution. Shell theory further predicts that in other scenarios, traditional normalization can have a strongly negative impact on downstream classification tasks. Finally, shell theory predicts that the ideal normalization vector should be the mean of the test data; we term this modified normalization procedure, shell normalization.

Empirical results show a combination of shell normalization and distinctive-shell discovery is effective on many machine learning tasks.

Breaking the curse

Shell theory suggests the contrast-loss [3] constraints used to derive the curse may be a blessing. Unlike previous works that derive similar blessings [2], shell theory's formulation also allows the curse to be re-derived. The result is a unifying framework for interpreting high dimensions.

We begin by explaining the curse's origins.

1. Explaining contrast-loss: In high dimensions all i.i.d outcomes of a single generative processes are almost-surely be equidistant to each other. This phenomenon is often termed contrast-loss and was first derived in [3].
2. Contrast-loss to curse: The authors of contrast-loss [3] (reasonably) argue that there must exist a distribution-of-everything. They further suggest that most instances are i.i.d. outcomes of that distribution. If so, the authors then claim that contrast-loss would make almost-all instances equidistant to one another; and thus, machine learning in high dimensions would be impossible.
3. Conceptual flaw in the curse's claim: Machine learning can be interpreted as an attempt to classify instances by mapping them to their generative process of origin, with class labels acting as symbolic representations of individual generative processes. If, as claimed by the authors of the curse, that there exist only one generative process, there would be only one label and classification would be ill-defined in both high and low dimensions. Thus, it is inappropriate to argue that high dimensions are cursed using a model with only one generative process.

Shell theory's perspective on the curse.

1. Explaining contrast-loss intuitively: To shell theory, contrast-loss is a natural result of the vastness of high dimensional sample spaces. In such vast spaces, two instances independently generated instances should not be coincidentally close to one another. Thus, if instances are independent outcomes of a single generative process, they can reasonably be expected to be equidistant to one another.
2. Contrast-loss is a blessing: Shell theory uses the fact that coincidental similarity is almost-impossible in high dimensions to show that in the context of a hierarchical generative process, the statistical dependencies that arise from sharing a parent generative process, will give rise to distinctive-shells that encapsulate instances of individual semantics, while excluding almost-all other instances. From this perspective, contrast-loss turns from a curse into the origins of our classification constraints (semantic manifolds).
3. Reconciling the curse: From shell theory's perspective, the curse arises in a degenerate case of the hierarchical generative process, where the generator-of-everything directly creates instances without intermediate child generators. As shell theory considers semantics to be symbolic labels for individual generative processes, classification is innately impossible in this degenerate case where there is only one generative process.

Our hope is that shell theory will act as an intuitive framework for interpreting high dimensions; and provide the internal consistency that is missing in the current curse-blessing framework.

Algorithms

As explained previously, shell theory predicts that traditional normalization will fail in unbalanced datasets where training and testing data derive from very distributions. However, shell normalization is still effective. This allows for very effective one-class learning and anomaly detection.

One-class Learning

The goal of one-class learning is to find the semantic manifold that encapsulates all instances of a given class, while excluding all other instances. Shell theory predicts that the semantic manifold is the distinctive-shell and the distinctive-shell is especially distinctive if shell normalization is applied.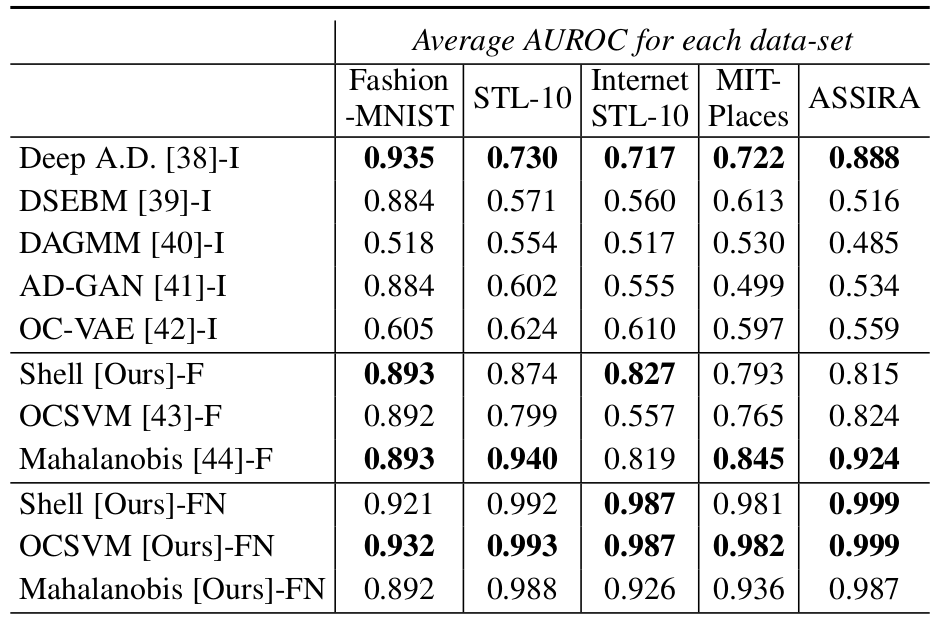

Anomaly Detection

Interestingly, a modified robust least squares that iteratively guesses the appropriate normalization followed by a fitting of distinctive-shells, leads to a rather effective anomaly detector. We term the algorithm re-normalization. Below is the anomaly based ranking of airplane images crawled from the internet. Anomaly scores decrease from left to right, top to bottom. Shell based anomaly detection provides rankings which are noticeably more consistent.