LVAD: Locally Varying Anomaly Detection
Introduction
Unsupervised anomaly detection on high-dimensional data like images is notoriously unstable. We argue this is because traditional density-based techniques are ill-conditioned in high dimensions; and low dimensional embedding schemes often eliminate the variations which separate normal from anomalous instances. Rather than use a traditional global embedding, LVAD projects instances of each cluster to a local embedding which, as explained by shell theory [1], is optimal for deciding cluster membership. The various cluster membership scores are agglomerated into a mutual affinity score, with anomalies being instances whose mutual affinity to other data-points is surprisingly low. The resultant anomaly detector is robust to a wide range of datasets and anomaly percentages.Paper, resNet50 features, raw images, Github (Python Code), Video, ECCV Poster
Classic Anomaly Detection meets High Dimensions

Anomaly detector: Kernel Desnity Estimation (KDE) with PCA.
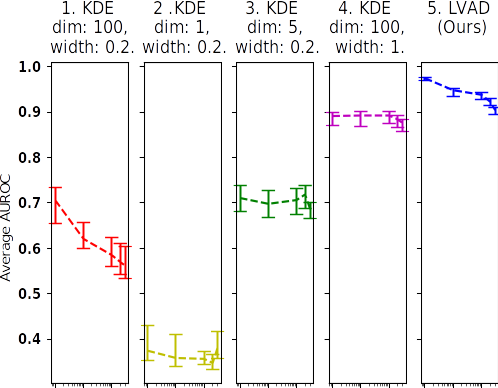
Dataset: STL-10. Image Representation: ResNet features.
Anomaly detector: Kernel Desnity Estimation (KDE) with PCA.
Dataset: MNIST. Image Representation: Raw Pixels.
Density is ill-defined in high dimensions: Classic anomaly detection assumes that because anomalies are rare, anomalous regions of the sample space will be less densely populated than normal regions. This assumption breaks down when applied to high dimensional data like images. This is because the volume of a sample space increases exponentially with the number of dimensions. Thus, high-dimensional sample spaces tend to be so huge that they are sparse everywhere. This renders traditional, density-based anomaly detectors ill-conditioned.
Dimensionality reduction is not the solution: The problem posed by high dimensions is widely acknowledged in machine learning literature, which typically advises the re-establishment of density, through embedding the data in a low dimensional space. The dimensionality reduction is typically achieved by discarding data variations that are deemed less important. However, anomalies are, by definition, a small fraction of the dataset; and thus, the variations that distinguish normal from anomalous instances are also a small fraction of overall of the total variations. Thus, dimensionality reduction often removes the variations needed to distinguish anomalies.
Experiments: Figures (A) and (B), above illustrate the performance of a naive anomaly detector, which consist of a PCA dimensionality reduction, followed by a kernel density estimation. While the detector does not fail completely, it's performance fluctuates enormously with dataset, parameter choice and anomaly percentage, a phenomenon that is mirrored in many, more advanced, anomaly detectors.
- Figure (A1) accords with conventional wisdom. The relative high number of dimensions means density and thus the anomaly detector is ill-conditioned, with the detector failing rapidly as the anomaly percentage increases.
- Figure (A2,A3) illustrates the problem with conventional wisdom. Lowering the number of dimensions makes the anomaly detector fail on easy, low anomaly percentage case; and only works on the more diffcult, high anomaly percentages. The performance reversal is likely because in the low anomaly case, the variations between normal and anomalous instances is a very small a fraction of the total variation; and thus, was elimnated by the PCA embedding. Such performance reversal is displayed by other anomaly detectors.
- Figure (A4) shows the effects of combining a large number of dimensions with a huge density kernel. The sparsity induced by using many dimensions is counteracted by the agglomerative effects of a large kernel, leading to an effective detector for the STL-10 data in Figure (A4). However, the agglomeration procedure is too coarse to accommodate the more difficult, MNIST data, illustrated in Figure (B4).
Our Approach
Assume clusters correspond to indepdent generative procesess: Let us assume local data clusters are outcomes of individual, high dimensional generative pro- cesses. Shell theory [1] suggests that instances of each generative process will be uniquely close to their mean. Thus, the likelihood an instance belongs to a spe- cific cluster can be determined from its distance to the cluster mean.
Multiple one dimensional embeddings, each responsible for seperating instances of its associated cluster from all other clusters: If shell theory is true, it suggests data should be embedded as a set of one-dimensional distance-from-mean projections, with each projection representing a space in which members of its associated cluster (generative process) are separable from all other instances.
Bottom up agglomeration of cluster membership statistics: Integrating shell theory [1] with Bayes Rule, we can infer the probability a given instance is a member of its associated cluster, from the sample density of its distance projection. Agglomerating the probabilities yields a statistical quantification of the affinity of each instance to the dataset. Instances with surprisingly low affinity scores are deemed anomalous. We term this Locally Varying Anomaly Detection or LVAD.
Decoupling of inference stability from number of dimensions: Unlike traditional anomaly detectors which infer class membership using all dimensions simultaneously, LVAD uses a bottom up inference scheme in which local cluster membership is inferred from individual, one dimensional projections. These inferences are then merged into an estimate of class membership. This effectively decouples inference stability from the number of projections, allowing LVAD to employ large numbers of local projections to model data variations as faithfully as possible. Figures (A) and (B) show LVAD is effective on a wide range of datasets, features and anomaly percentages.
Results: Experiments in the attached paper show LVAD's performance is exceptionally good. LVAD is stable across a wide range of anomaly percentages and datasets. Further, it displays the graceful degradation expected of robust systems, with high accuracy on easy tasks with low anomaly percentages; and a slow decline in accuracy as anomaly percentages increase. Some qualitative results are shown below.
The first anomaly (most normal anomaly) is highlighted in red.

crawled with search word "airplane".
Links:
[1] Shell Theory: A Statistical Model of Reality